Almost all software development problem requires a solid understanding of data structure. And learning data structure is essentials than learning syntax.

What is data structure:

“Data structure is a particular way of organizing data in a computer. ”

Why it is important:

“Bad programmers worry about the code. Good programmers worry about data structures and their relationships.”
― Linus Torvalds

This is the famous quote from Torvalds, Too bold, but true. A good developer should always know data flow inside the application and how to use the different data structures to maintain this flow more efficiently via correctly choosing format and type.

If you like more structure code and dev-documentation. Check out this website with more defined code example.

https://raufr.github.io/datadoc/

In this series, I will describe the different data structures and their used cased. The next series will contain more depth on each data structure. I used javascript for example, but all data structures can be implemented in all high-level programming languages.

Without more discussion, let’s dive into detail:

Most common data structures

* Arrays
* Stacks
* Queues
* Linked-List
* Trees
* Hashing
* Graph

Arrays

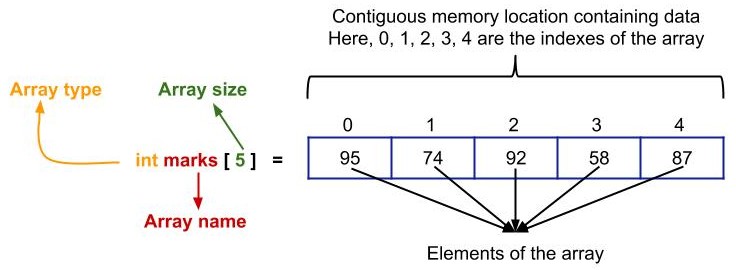
Most common data structure and widely used in the problem-solving world. Stack and Queues are derived from arrays. Arrays have 2 types:

1. One dimensional array
2. Multi dimensional array

Common operation with array:

• insert()
• get()
• delete()
• size()
• IndexOf()

The array is a data structure to store the same type of elements continuously.  You can use an array in the following use cases.

• Need access to other elements using the index.
• Know the size of the array before define memory.
• Much efficient when iterating sequentially.
• Take much less memory to compare to the linked list and other data structures.

Learn more about array

Stacks

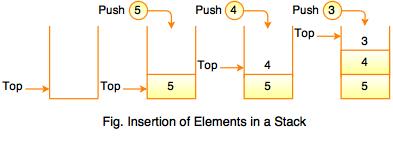
Did you remember the “Undo” operation in an application! Ever get curious about how it built! The stacks data structure used for this kind of operation.

!Idea: Use the last state of the application in memory as a way last saving element appears at the beginning, which called stacks. It is following LIFO(Last in first out) method

Common operation with Stacks:

• push()
• pop()
• isEmpty()
• top()

Some used case of stacks

• Expression evaluation and syntax parsing.
• Finding the correct path in the maze using backtrack
• Runtime memory management
• Recursion function .

Learn more about Stacks

Queue

Same as stacks but have an opposite mechanism called FIFO (first in first out). Very useful on serialize operation.

Common operation

• EnQueue()
• DeQueue()
• isEmpty()
• Top()

Used Case:

• Used queue when you want order and serialize data.
• Process in FIFO operations
• If you want add/remove data from start and finish, queue is much efficient

Linked List

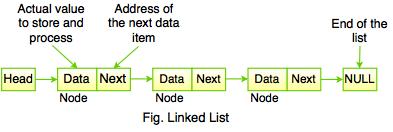
A linked list is another important linear data structure that might look similar to arrays at first but differs in memory allocation, internal structure and how basic operations of insertion and deletion are carried out.

A linked list is like a chain of nodes, where each node contains information like data and a pointer to the succeeding node in the chain. There’s a head pointer, which points to the first element of the linked list, and if the list is empty then it simply points to null or nothing.

There are two types of Linked List

• Unidirectional
• Bi-directional

Basic operations:

• insertAtend()
• insertAtHead()
• delete()
• deleteAtHead()
• search()
• isEmpty()

Used Cases:

• When the developer needs constant time for insertion and deletion.
• When the data dynamically grows.
• Do not access random elements from the linked list.
• Insert the element in any position of the list.
• Develop the buffer memory.
• Represent a deck of cards in a game.
• Browser cache which allows to hit the BACK button.
• Implement Most Recently Used (MRU) list.
• Undo functionality in Photoshop or Word.
• Easier to delete the node from doubly linked list.
• Can be iterated in reverse order without recursion implementation.
• Insert or remove from double-linked lists faster.

Tree

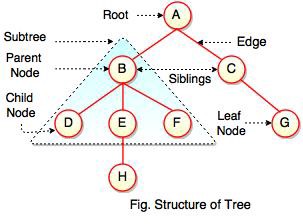
A tree is a hierarchical data structure consisting of vertices (nodes) and edges that connect them. Trees are similar to graphs, but the key point that differentiates a tree from the graph is that a cycle cannot exist in a tree.

The following are the types of trees:

• N-ary Tree
• Balanced Tree
• Binary Tree
• Binary Search Tree
• AVL Tree
• Red Black Tree
• 2–3 Tree

Used Cases:

• Find name in the phone book.
• Sorted traversal of the tree.
• Find the next closest element.
• Find all elements less than or greater than a certain value.
• File systems.
• Database operations.
• When the developer wants access the recent data easily.
• Allow duplicate items.
• Simple implementation and take less memory.
• When the application deals with a lot of data, use the tree.
• When the developer wants to control the tree height outside -1 to 1 range.
• Fast looking element.

Hash Table

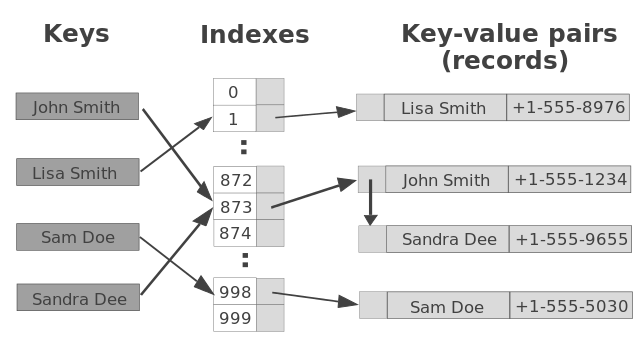
Hashing is a process used to uniquely identify objects and store each object at some pre-calculated unique index called its “key.” So, the object is stored in the form of a “key-value” pair, and the collection of such items is called a “dictionary.” Each object can be searched using that key. There are different data structures based on hashing, but the most commonly used data structure is the hash table.

The performance of hashing data structure depends upon these three factors:

• Hash Function
• Size of the Hash Table
• Collision Handling Method

Used Cases:

• Constant time operation.
• Inserts are generally slow, reads are faster than trees.
• Hashing is used so that searching a database can be done more efficiently.
• Internet routers use hash tables to route the data from one computer to another.

Graphs

A graph is a set of nodes that are connected to each other in the form of a network. Nodes are also called vertices. A pair(x,y) is called an edge, which indicates that vertex x is connected to vertex y. An edge may contain weight/cost, showing how much cost is required to traverse from vertex x to y.

Types:

• Undirected Graph
• Directed Graph

In a programming language, graphs can be represented using two forms:

• Adjacency Matrix
• Adjacency List

Common graph traversing algorithms:

• Breadth First Search
• Depth First Search

If you think this article is helpful, share with your friends.

Let me know if I have missed any type.

Happy Coding.